Transformation Nets

As model transformations play a key role in model driven development, several dedicated languages have emerged that allow to define and execute transformations between source and target metamodels. Compared to general purpose programming languages, model transformation languages provide a layer of abstraction by allowing to manipulate models in terms of their abstract syntax given by its metamodel. Different kinds of model transformation language approaches range from purely imperative styles allowing to define how an transformation is carried out, to fully declarative transformation definition styles focusing on what a transformation's output should be like, according to a certain input. Declarative approaches (i.e. graph transformations) are typically based on defining rules that are later on interpreted by an execution engine to produce the desired result. Hence, the actual transformation execution as well as the order of rule application generally need not be handled by the user. Declarative rules typically consist of a semantically corresponding source and target patterns, whereby for each match of the source pattern in the input model, a target pattern is instantiated in the output model.

Imperative approaches are similar in usage to traditional programming languages and allow the developer to explicitly manipulate transformation execution state and control flow. They offer great flexibility and ease of use, but the programming model does not support an intuitive alignment of concepts as known schema integration tasks, and often it is necessary to manually implement what a more succinct declarative description would achieve. However, what a declarative approach gains in abstraction, it loses in flexibility. Naturally, declarative specifications are convenient language constructs for recurring transformation tasks, but for “tricky” problems, a rule-based paradigm can become unwieldy. In general, existing declarative approaches, are governed by an underlying execution procedure implemented in the respective transformation engine. In our opinion, this rigidness is the main cause for trouble when attempting to solve tricky problems with declarative approaches. As the actual transformation definitions can be seen as merely parameterizing an intrinsically rigid, pre-defined procedure, we view declarative approaches as data-oriented, in the sense that they specify how input data is mapped onto output data.

As opposed to declarative approaches, imperative approaches express transformations on a very fine-grained level, which is flexible but incurs explicit handling of control flow without support for the alignment of concepts as it is prevalent in schema integration tasks, for instance. Instead of specifying what input data is mapped onto what output data, imperative approaches follow a procedure-oriented paradigm and allow to algorithmically define a function that computes the output model from the input model.

We propose to rethink the notion of models as input and output data which is subject to a transformation that is seen either as an explicit or implicit procedure, but understand a transformation as a process. In a process-oriented view, a transformation execution is carried out by interacting entities that control streams of information from source to target models. The flowing information stems from the models themselves, and the actual transformation logic is made up by the behavior of individual entities and their interaction which each other.

Consequently, we propose the transformation net formalism, which is based on conditional, colored Petri-nets, to represent transformation processes. Such an execution model provides the explicit statefulness of imperative approaches through markings contained in the net's places. The abstraction of control flow from declarative approaches is achieved as transitions can fire autonomously depending on their environment. To describe specific firing rules for transitions, we resort to pre/post rules known from graph transformations.

The transformation net formalism serves as a flexible execution environment to be targeted by generators of higher-level transformation languages, such that specific transformation and integration operators can be defined using the semantics offered by transformation nets. As symbolically displayed in Figure 1, the “compilation” step produces a transformation net in its initial state (i.e. ready for execution) that uniformly represents models, metamodels and transformation specifications. The static parts of a transformation net that correspond to the transformation process’ inputs and outputs, are generated from models and metamodels, whereas the part that corresponds to the process’ execution logic is created from the integration specification by a custom generator for a certain higher-level language.

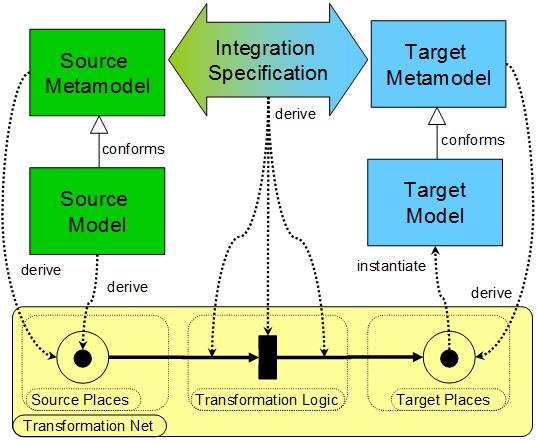
The gap between the modeling and the transformation net technical space is bridged by the mapping described in the following.

• Classes, references and attributes of metamodels are mapped to places of a transformation net.
• Objects , as instances of classes are mapped to one-colored tokens within a place that corresponds to the object’s class. The token’s color represents an object’s unique ID.
• Links between objects conforming to a certain reference are mapped onto two-colored tokens within a place that corresponds to the link’s reference. The two colors represent a link’s source (ring color) and target (center color) and stand for the ID of the linked objects.
• Values of attributes are mapped onto two-colored tokens within a place that corresponds to the values’ attribute. The two colors represent an object’s unique ID and the denoted value.

To complete the transformation net and to provide the actual process logic, a system of transitions and places has to be established that is capable of streaming tokens from the places corresponding to the input metamodels to places corresponding to the output metamodel. During execution, state information is explicitly provided by the markings of places, which makes it possible, to trigger transitions according to a certain runtime state, as opposed to only act upon data comprising the input model. The notion of triggering transitions according to runtime events or states is similar to the notion of point-cuts determining the execution of advice in aspect-oriented programming. Therefore, the following example shows how to incorporate a weaving mechanism on the language level and introduces a high-level integration language for which transformation net generation and execution is demonstrated.

The example deals with the specification of a transformation and its compilation into a net that finally executes the transformation process. The Figure below shows the source and target metamodels, as well as the input model and the desired output model. As shown, a transformation between these two metamodels has to transform array input models into linked-list output models.

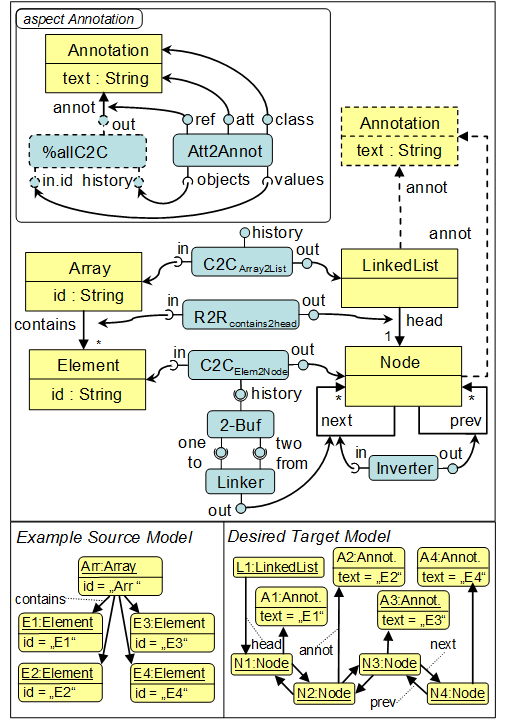
The transformation specification is given in an example language, whose operators stand for a certain processing entity, which has inputs and outputs by which operators can be assembled in a component-based way. For instance, the C2C (Class2Class) component takes objects from the "Element" class as input, and outputs them into the "Node" class. The C2C component offers another output port "history", of which all this components yet handled tokens can be accessed. The 2-Buf component connected to C2C's "history" sequentially fills an internal buffer of size two, which is again provided as output port. A Linker component takes the two objects in the buffer, and produces a link between them which is streamed into the "next" place. The Inverter component produces back-links the "next" place and streams them into the "prev" place.

Certain operators can also cross-cut a transformation specification: Because the target metamodel classes do not have ID attributes, these should be stored within an annotation for eventual round-tripping. This can be accomplished by the Att2Annot component, which crosscuts the transformation of every object and is therefore woven with every C2C component. The transformation specification is itself a model, and due to the component-like assembly, existing model weavers can be used to merge the aspect operator into the base transformation specification. The query in the aspect selects all C2Cs, with three additional sub-queries “in.id”, “history” and “out”, relative to the current C2C operator. The results of “in.id” and “history” are bound to the “values” and “objects” ports of the Att2Annot operator, which for every transformed object instantiates a new Annotation object (“class” port) which is linked up (“ref” port) with the according Node object and sets its text attribute (“att” port) to the value of the source objects “id” attribute. Additionally, the “Annotation” class is woven into the target metamodel, as indicated through the dotted lines in Figure 2. Thereby, the result of the “out” query determines the classes to which an “annot” reference will be added.

After the weaving process is carried out on the language level, generation takes place to produce a transformation net out of an integration specification. Thereby Petri-net patterns are instantiated according to the transformation net semantics of the operators and assembled according to the overall integration specification. The top of the figure shows a transformation net resulting from the above integration specification. The transitions’ firing rules are defined with a visual notation that uses pattern-filled tokens that can match for certain input tokens and produce output tokens whose color is either different, the same, or a combination (two-colored tokens) of the matched input colors. Places marked as “ordered” index contained tokens and provide them in a sorted fashion. Furthermore, according to the multiplicity of a reference, a place (e.g. “head”) can have a capacity, which constrains the amount of tokens a place can hold.

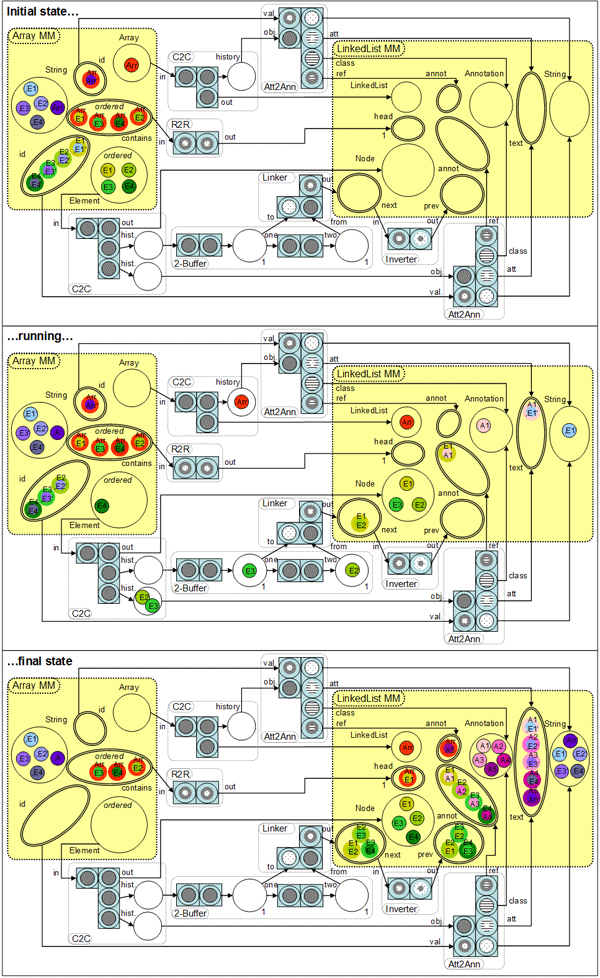
The middle and the bottom of the below figure show the transformation net during execution and in its finished configuration. For instance, one can see how the tokens streamed through the C2C component are stored in its “history” place. The 2-Buf component takes in these tokens and fills its two-place buffer. Once the buffer is full, the Linker component’s transition can fire and empty the buffer, producing a two-colored token which is streamed into the “next” place. Thereby it is to note, that the creation of two-colored tokens for the “next” link is based on a certain state of the execution, rather than on the input model alone.

Furthermore, one can see how the previously weaved operators form Petri-net patterns that become active after an Array or Element token was streamed. As an example, in the “running” net, the lower Att2Annot pattern has already created an annotation with the according value for the “E1” object, and is currently enabled to do the same for “E2” and ”E3”. Once the transformation process has finished, the final net configuration is used to instantiate a model that conforms to the target metamodel.